My Cryptography Final Project

For my Cryptography class, we were required to do a final project. In this post, I’ll talk about the different parts of my project and how I wrote them.

My program is a trivial implementation of RSA encryption in Rust. It will choose a random p and q and using them, it will generate a private and public key. It will then ask the user for input, after which it will encrypt and decrypt the input.

The source code for this project is hosted on Github if you’re curious.

I’ll go through the functions in the order I wrote them in, but I’ll leave the main function for last.

Coming into this project, I knew that I wasn’t going to be generating a cryptographically secure function. Thus, there are plenty of vulnerabilities (timing attacks, for example) that could be exploited in this library. Since I was also using this project as an opportunity to learn Rust, I spent more time learning how to use Rust than I did securing my cipher.

The generate_prime function

The first function I wrote is generate_prime. In order to create public and private RSA keys, you start by generating 2 random prime numbers. In order to find one such number, I opted for the brute-force method of picking a random number and checking if it’s prime. If it is, use it. If not, get a different number.

While the function returns a signed 128-bit integer, the random number will only be between 1 and $2^{32}$. This is because using $2^{64}$ as the maximum possible value the caused the program to take too long to find a prime number. $2^{32}$ ended up being my sweet spot.

fn generate_prime() -> i128 {
    loop{
        let base: i128 = 2;
        let number = rand::thread_rng().gen_range(1..=base.pow(32));

        if primes::is_prime(number.try_into().unwrap()){
            return number;
        }else{
            continue;
        }
        
    }
}

The mod_pow function

I tried implementing my own mod_pow function, but due to multiple difficulties (mostly due to my lack of knowledge of Rust), I decided to just use the prebuilt BigInt::modpow function from the num crate. My mod_pow function acts as a wrapper for this function, as I use it multiple times.

The problem I faced is that the BigInt::modpow function operates on BigInts, not on i128s. As a result, I had to convert my i128s into BigInts, then back again.

The BigInt class doesn’t contain a listed function for returning a i128 with the same value. It does contain a function to return u64s, so I made my function return these, as they can be cast to i128s if needed.

fn mod_pow(base: i128, exp: i128, modulus: i128) -> u64 {
   
    // **Warning**: Converting from BigInts to u64, so there may be some slight data loss

    let result = BigInt::modpow(&BigInt::from(base), &BigInt::from(exp), &BigInt::from(modulus));
    
    let (_a, b) = result.to_u64_digits();
    
    b[0]
}

The input_int function

Throughout my testing, I needed to be able to input my own values for numbers a few times. I had also originally planned on letting the user input their own private key to decrypt a message, but I decided to cut this out due to time constraints.

This function has remained as a relic of that. It makes this function more modular and helps if I choose to re-implement this functionality in the future.

Most of the code here is taken from the Rust tutorial for programming a guessing game.

I tried playing with the parse function elsewhere to let the user choose between the multiple functions I had planned for, but I couldn’t get that code working within my deadline, so I scrapped that.

fn input_int() -> i128 {
    loop{
        let mut guess = String::new();

        io::stdin().read_line(&mut guess).expect("Failed to read line");

        match guess.trim().parse(){
            Ok(num) => return num,
            Err(_) => {
                println!("Please enter a valid number!\n");
                continue;
            },
        };
    }
}

The main function

My main function is based on a textbook implementation of RSA (the link provided leads to a good handout which explains basic RSA, though it wasn’t the textbook we used in class).

It begins by generating two primes, p and q. It calculates n as $n=p\times q$ and $\phi$ as $(p-1)(q-1)$. e is always set to 65537, a common exponent in RSA encryption. d is set to the inverse mod of e mod $\phi$. Like with the mod_pow function, I chose to use a prebuilt modinverse function. Due to an unfixed issue in the library, however, I wasn’t able to use u64s throughout the program, as the modinverse function currently doesn’t work with unsigned numbers. This is why the program uses i128s instead of u64s in most cases.

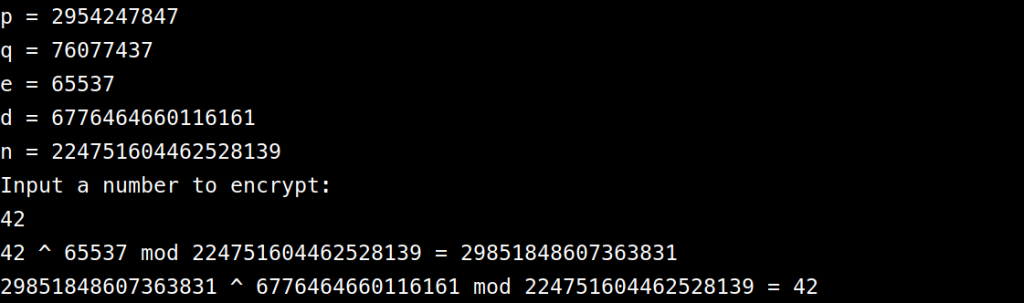
Finally, I ask the user for input and encrypt and decrypt it as normal ($p^e\pmod n=c$, $c^d\pmod n=p$).

fn main(){

    let p : i128= generate_prime();
    let q : i128 = generate_prime();

    let n : i128 = p * q;

    let phi : i128 = (p - 1) * (q - 1);

    let e: i128 = 2_i128.pow(16) + 1;

    let mut d:i128 = 0;

    let does_exist = modinverse(e, phi);

    match does_exist {
        Some(x) => d = x,
        None => panic!("modinverse() didn't work as expected"),
    }


    
    println!("p = {}", p);
    println!("q = {}", q);
    println!("e = {}", e);
    println!("d = {}", d);
    println!("n = {}", n);

    println!("Input a number to encrypt:");
    let p:i128 = input_int();
    let c:u64 = mod_pow(p, e, n);

    println!("{} ^ {} mod {} = {}", p, e, n, c);

    let decrypted:u64 = mod_pow(c.into(), d, n).into();

    println!("{} ^ {} mod {} = {}", c, d, n, decrypted);

}

Conclusion

That’s it! I hope you were able to learn something from my project! If you have any questions, feel free to open an issue or leave a comment on this post!